Marktneutralität oder wie man den Markt mit geringem Risiko schlagen kann (Teil 1)
Wie wir alle wissen, gibt es keinen “Heiligen Gral“, aber wenn man mich bitten würde, zu sagen, was dem Gral am nächsten kommt, würde ich definitiv „Marktneutralität“ antworten. Marktneutralität bedeutet, dass die Renditen eines Portfolios unabhängig von der Marktsituation sind. Sie erlaubt es uns, mehr zu verdienen, unabhängig davon, ob der Markt fällt oder wächst, und die Drawdown-Perioden eines solchen Portfolios dauern viel kürzer als bei Standardansätzen.
In dieser Artikelserie erfahren Sie, wie man marktneutrale Anlageportfolios zusammenstellt, deren Renditen viel höher und deren Drawdownzeiten viel geringer sind als beim S&P500. (auf die Grafiken Klicken zum zoomen)
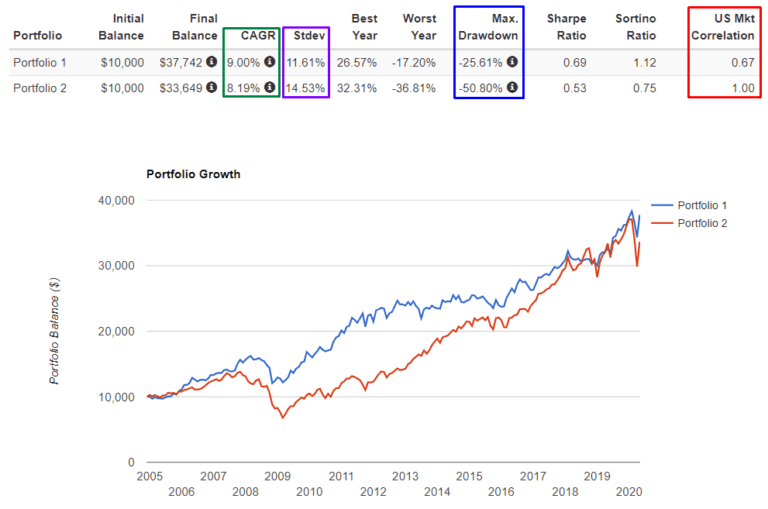
Hier ein Beispiel eines marktneutralen Portfolios:
Achten Sie auf die Rendite (mehr als das 2,8-fache) und den maximalen Drawdown (weniger als das 2,9-fache) des Portfolios im Vergleich zum S&P500, bei fast identischer Standardabweichung „Stdev“.
Dieselbe Standardabweichung bedeutet, dass beide Portfolios bei natürlichen, nicht krisenbedingten Marktschwankungen vor dem Hintergrund einer Krise in gleicher Weise nach oben und unten gehen.
Das Portfolio wird mit Hilfe von ETFs aufgebaut – den bequemsten Instrumenten für den durchschnittlichen Anleger.
Schauen wir uns an, was diese Marktneutralität ist und warum sie so gut funktioniert:
Ein Maß für die Marktorientierung ist die Korrelation. Die Korrelation ist, grob gesagt, die Ähnlichkeit der Dynamik verschiedener Werte. Sie wird im Bereich von +1 (völlige Identität der Dynamik) bis -1 (das vollständige Gegenteil der Dynamik) gemessen, eine Korrelation von 0 zeigt die Unabhängigkeit der Werte von einander an.
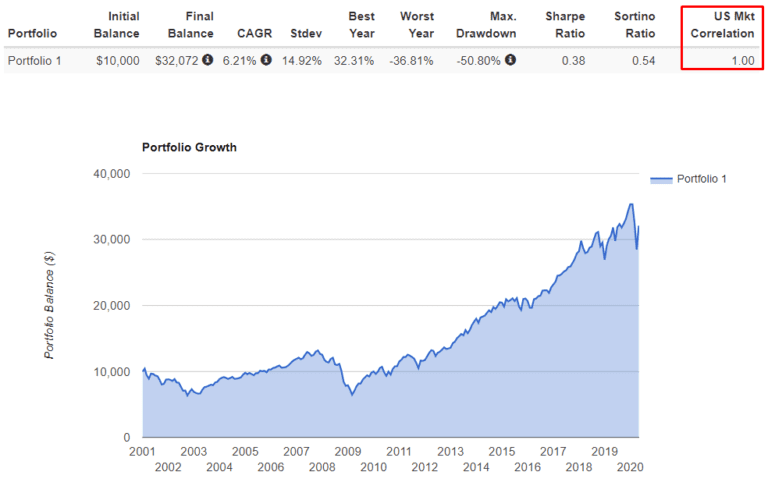
Zunächst wird bestimmt, was nicht marktneutral ist. Zum Beispiel der S&P500. Da der S&P500 der Hauptindikator für die Weltwirtschaft ist, wird er selbst oft als „Markt“ bezeichnet. Dementsprechend spiegelt die Dynamik des S&P500 die Marktdynamik am vollständigsten wider. Lassen Sie uns einen genaueren Blick darauf werfen:
Die Grafik verwendet „Gesamtrenditen„, was bedeutet, dass die Grafik nicht nur das Wechselkurswachstum des Instruments berücksichtigt, sondern auch die gezahlten und in das Instrument reinvestierten Dividenden.
Sobald wir verstanden haben, was eine Korrelation von +1 ist, wollen wir uns andere Beispiele mit einer Korrelation von weniger als +1 ansehen.
Der QQQ und der DIA von ETFs sind fast vollständig mit dem S&P500 korreliert, da sie auch Wertpapierindizes innerhalb der amerikanischen Wirtschaft sind. Sie mögen zwar eine unterschiedliche Zusammensetzung der Unternehmen haben, aber aufgrund ihrer strukturellen Ähnlichkeit ist ihre Dynamik fast identisch.
Werfen wir nun einen Blick auf den Chart von Gold (etf GLD) im Gegensatz vom S&P500 (SPY) mit einer Korrelation nahe Null.
Wir können eine sehr schwache Korrelation feststellen. Manchmal laufen sie nebeneinader, manchmal gegensätzlich, oft unabhängig voneinander.
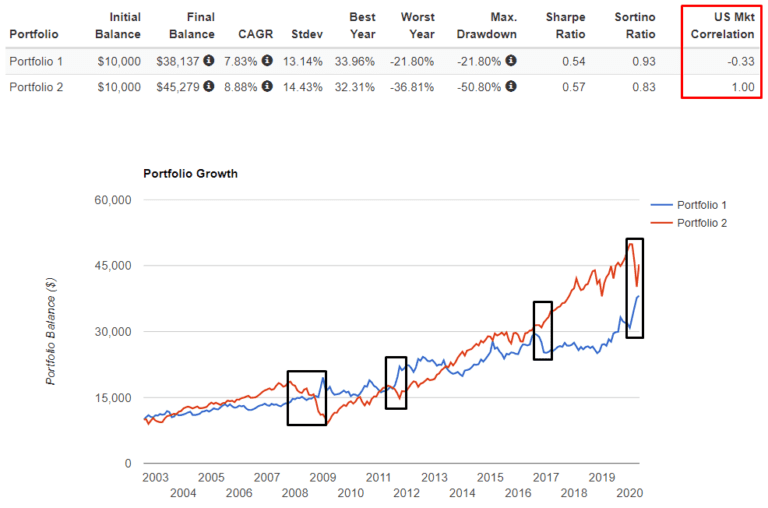
Im Folgenden finden Sie eine Tabelle der US-Schatzbriefe (etf TLT) im Vergleich zum SPY. Wir beobachten eine negative Korrelation, die oft in entgegengesetzter Richtung zueinander verlaufen, insbesondere bei Marktrückgängen (gekennzeichnet durch schwarze Quadrate).
Es gibt einen klaren fundamentalen Grund, warum sich die Schatzbriefe so verhalten. Wir werden dies in den folgenden Artikeln ausführlich erörtern.
Nun, da wir die Korrelation als ein Maß für die Marktorientierung verstehen, können wir die „Gralität“ dieses Wissens offenbaren:
Wir müssen im Portfolio die maximale Anzahl der am wenigsten voneinander abhängigen, vorzugsweise sogar entgegengesetzten Erträge sammeln.
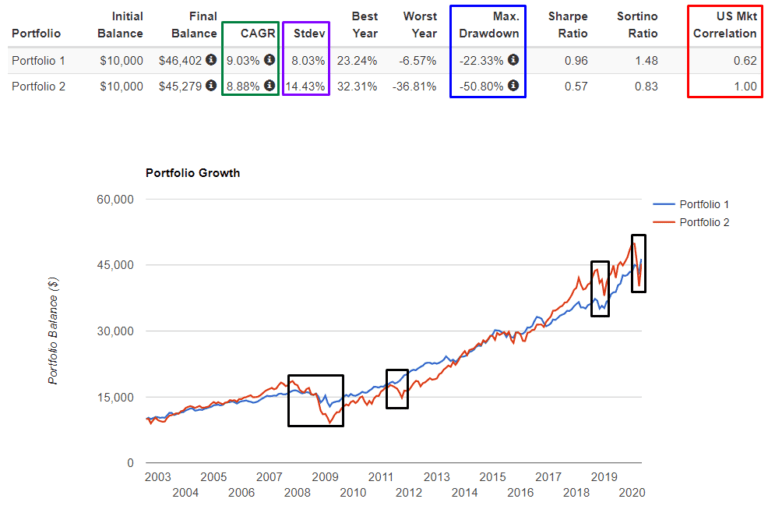
In unserer Liste sind die am wenigsten abhängigen und einander entgegengesetzten Renditen SPY (+1) und TLT (-0,35). Kombinieren wir sie miteinander in einem gleichen Verhältnis von 50% zu 50% und sehen, was passiert. Zur Verdeutlichung werden wir die resultierende Grafik mit SPY 100% vergleichen.
Sie können sehen, dass das „Wunder der geringsten Korrelationen“ eingetreten ist. Wir haben eine Rendite (grün hervorgehoben) wie im S&P500, während der maximale Drawdown (blau hervorgehoben) mehr als zwei Mal niedriger geworden ist als im S&P500. Und die Standardabweichung (violett hervorgehoben) hat sich verringert. Unser Portfolio ist viel stabiler geworden, weniger durchhängend und hat keine Renditen verloren!
Wie Sie sehen können, heben sich inverse Korrelationen gegenseitig auf und stabilisieren das Portfolio.
Wenn wir etwas Ähnliches bei den weniger invers korrelierten Reihen SPY (+1) und GLD(+0,06) machen, werden wir sehen, dass das „Wunder der geringsten Korrelationen“ viel schwächer ist.
Die Rendite ist etwa gleich hoch wie die von SPY/TLT, aber der Drawdown ist höher und die Standardabweichung ist ebenfalls höher.
Wenn wir bei Instrumenten mit einer sehr hohen Korrelation ähnlich vorgehen, wird es überhaupt kein „Wunder der geringsten Korrelationen“ geben.
In der Tat sind Rendite, Standardabweichung und Drawdown eines sehr ähnlichen QQQ + SPY ungefähr gleich hoch wie die eines reinen SPY, was ein Beweis für unsere Hypothese „vom Gegenteil“ sein könnte.
Lassen Sie uns nun über die Qualität des Portfolios sprechen:
Wir sind an mehreren Parametern interessiert: Jahresertrag, Standardabweichung, maximaler Drawdown und Korrelation zum Markt. Aber diese Parameter sind nicht nur einzeln wichtig, sondern auch ihr Verhältnis zueinander.
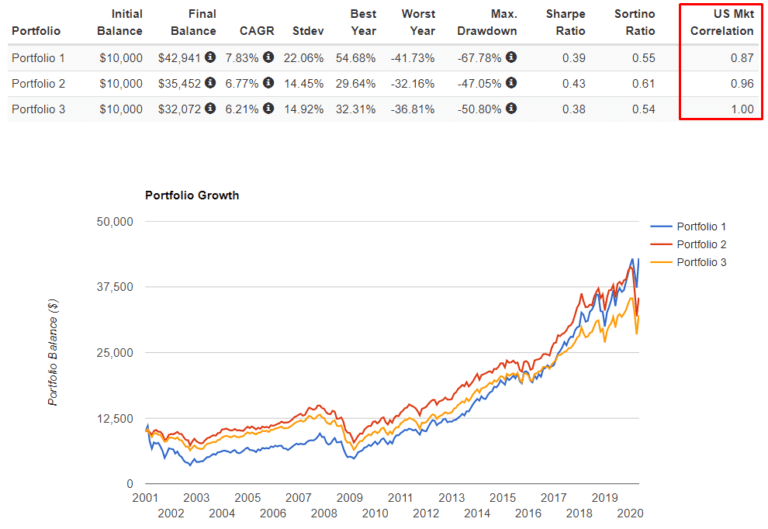
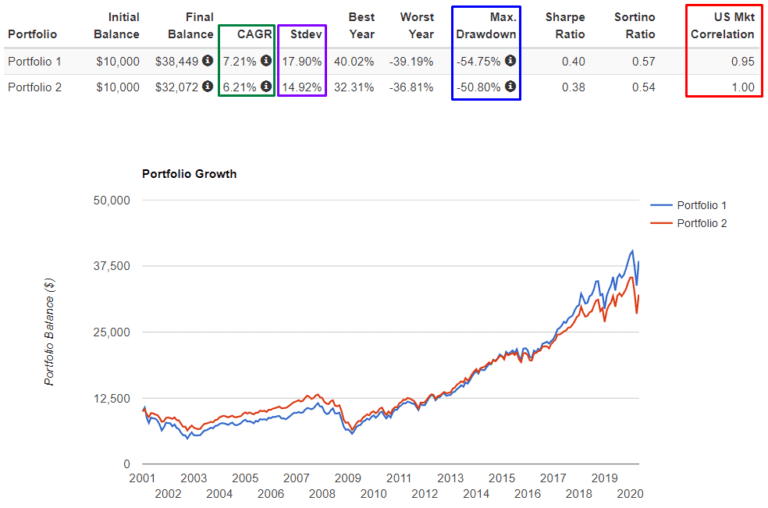
Vergleichen wir die oben aufgeführten Portfolios für den gleichen Zeitraum miteinander, damit dies korrekt ist.
Das erste Portfolio (SPY-TLT) ist pro Risikoeinheit viel stabiler als das zweite (SPY-GLD) und noch stabiler als das dritte (SPY-QQQQ). Wir können dies anhand der Verhältnisse Rendite/Standardabweichung (im Folgenden “eSharpe”) und Rendite/Maximaler Abschlag (im Folgenden “CALMAR”) besser verstehen.
eSharpe (easy Sharpe) ist eine leichtere Version des Sharpe-Verhältnisses, aus dem die Dynamik des risikofreien %-Satzes entfernt wurde.
- Erstes Portfolio: 8.7 / 8 = 1.09 eSharpe und 8.7 / 22.3 = 0.39 CALMAR
- Zweites Portfolio: 9 / 11.6 = 0.77 eSharpe und 9/25, 6 = 0.35 CALMAR
- Drittes Portfolio: 10.5 / 15.6 = 0.67 eSharpe und 10.5 / 50 = 0.21 CALMAR
Je höher die Zahl, desto besser. Nun sehen wir, dass das erste Portfolio um das 1,09 / 0,67 = 1,63-fache der eSharpe-Metrik und um das 0,39 / 0,21 = 1,86-fache der CALMAR-Metrik effizienter ist als das dritte.
Achten Sie auf die rote Box, in der die Korrelationsverhältnisse für den Markt angezeigt werden, und Sie werden verstehen, warum dies geschieht.
Wenn Ihnen die Historie seit 2005 nicht ausreicht,
dann lassen Sie uns nicht durch die etf testen, sondern durch Total-Return-Indizes, deren Daten bereits seit 1978 verfügbar sind:
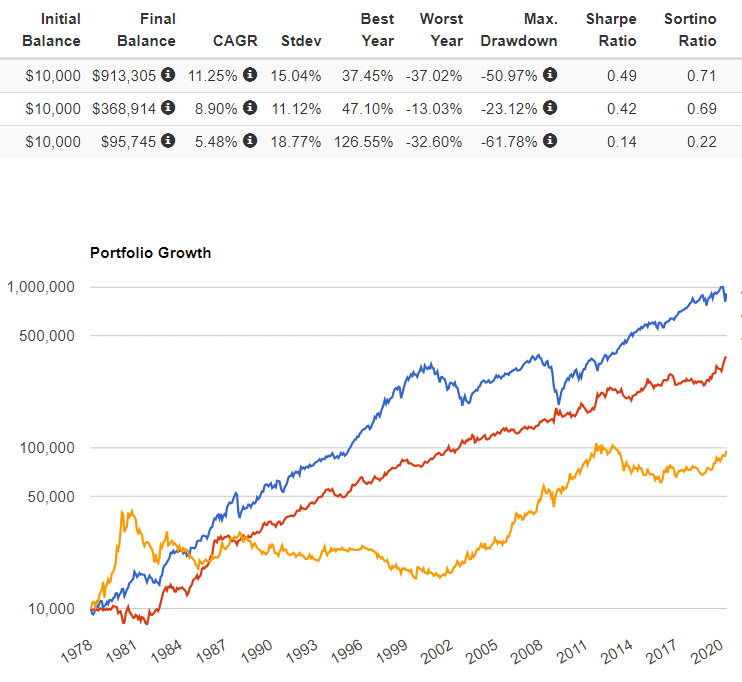
Large cap (analog dem SPY) (blau), Long treasures (analog dem TLT) (rot), Gold (analog dem GLD) (gelb)
Jetzt können wir alles mit der gleichen Portfoliostruktur kombinieren, die wir getestet haben.
Vergleichen Sie selbst die eSharps- und CALMAR-Verhältnisse für jedes Portfolio und Sie werden sehen, dass das „Wunder der geringsten Korrelationen“ auch über einen Zeitraum von mehr als 40 Jahren wirklich funktioniert.
Und nun schauen Sie sich das allererste Diagramm in diesem Artikel noch einmal genau an. An dieser Stelle haben Sie bereits ein kleines Puzzleteil namens „Marktneutralität“. In den folgenden Artikeln werden wir das gesamte Puzzle vollständig zusammensetzen, und Sie werden jedes Element der Marktneutralitäts-Strategie verstehen.
Alle Berechnungen werden im portfoliovisualizer durchgeführt. Wenn Sie auf den Link klicken, können Sie alle Ergebnisse selbst überprüfen: https://www.portfoliovisualizer.com/backtest-portfolio#analysisResults
Bis bald und viel Erfolg in Ihrem Geschäft
Euer InsiderWeek Team
Neugierig, mehr zu erfahren?
Hole dir das Buch von Max Schulz und lade es dir noch heute kostenlos herunter!